|
Markowitz - Grundlagen der modernen Portfoliotheorie

Markowitz zeigt, dass es nicht ausreicht, Risiko und Rendite der einzelnen Aktien isoliert zu betrachten. Vielmehr müssen die Korrelationen zwischen den jeweiligen Aktien untersucht werden, also das Ausmaß an Gleichförmigkeit der jeweiligen Kursverläufe. Wie Markowitz nachweist, ist ein Aktienportfolio umso schlechter diversifiziert, je stärker die Kurse der darin enthaltenen Aktien positiv korrelieren, also je gleichförmiger sie sich nach oben oder unten entwickeln. Je schlechter die Diversifikation eines Aktienportfolios ist, desto sensibler reagiert es auf Markteinflüsse.
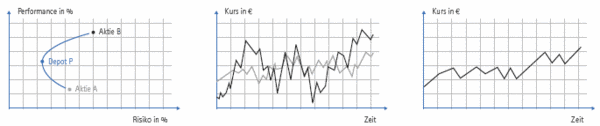
Die nachfolgenden Abbildungen illustrieren die positive Folge dieses Zusammenhangs: Diversifikation führt zur Risikominimierung. Dargestellt sind Risiko und Renditeerwartung der Aktie A, der Aktie B und eines Depots, das aus den Aktien A und B zusammengesetzt ist. |

Das Risiko/Rendite-Diagramm zeigt, dass die risikoreiche Aktie B exzellent zur Risikoreduktion des Gesamtdepots geeignet ist. Zwar ist Aktie A isoliert betrachtet risikoärmer als Aktie B, jedoch zeigt die Analyse, dass das gemischte Depot, bestehend aus Aktie A und Aktie B, deutlich risikoärmer ist als ein Depot, das ausschließlich aus Aktie A besteht. |
Portfolio statt Einzelfondsverkauf

Damit sind wir bei der zentralen Entdeckung von Markowitz: Ein risikoarmes Depot kann durch die Hinzunahme eines geeigneten risikoreichen Wertpapiers noch risikoärmer werden. In unserem konkreten Beispiel liegt das daran, dass die Kursentwicklung der risikoreichen Aktie B anderen regionalen und wirtschaftlichen Einflüssen (geopolitisch, branchenspezifisch) ausgesetzt ist als der Kurs der Aktie A. Deshalb kann eine Mischung der beiden Werte die Kursschwankungen glätten bzw. gering halten.
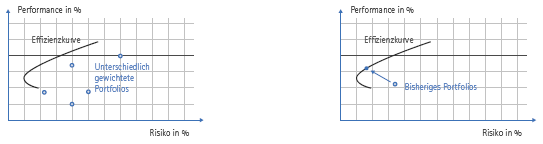
Was bisher beispielhaft anhand der zwei Aktien A und B beschrieben wurde, gilt natürlich auch in Bezug auf die Zusammenstellung vieler Wertpapiere (Portfolio). Je nach prozentualem Anteil der einzelnen Wertpapiere sind theoretisch nahezu unendlich viele verschiedene Depots denkbar. Abhängig von der Gewichtung der Wertpapiere im Depot verändern sich dabei Risiko und Rendite des gesamten Depots. |
Wann ist ein Fonds effizient?

Die Menge der effizienten Depots ist im Risiko/Rendite-Diagramm nach oben hin begrenzt. Diese obere Grenze wird Effizienzgrenze genannt (in der Abbildung als Effizienzkurve bezeichnet). Ein Depot, das auf der Effizienzgrenze liegt, nennt man effizient. Effiziente Depots haben bei einem bestimmten Risiko die höchste Renditeerwartung bzw. bei einer bestimmten Renditechance das kleinste Risiko. Es existiert dann kein anderes Depot, das bei einem bestimmten Risiko mehr Renditechancen bietet bzw. kein Depot, das bei mindestens gleichen Renditechancen weniger Risiko birgt. 
|
Komplexe Rechenverfahren

Zur Berechnung des Markowitz-Modells müssen die zu erwartenden Renditen (basierend auf historischen Wertentwicklungen), die Varianzen der betrachteten Wertpapiere und die Korrelationen zwischen ihnen bekannt sein oder mittels anerkannter Schätzverfahren prognostiziert werden. Die Berechnungen, die dabei durchgeführt werden müssen, sind so komplex, dass sie nur mit Hilfe leistungsfähiger Soft- und Hardware erfolgen können. Darüber hinaus sind umfangreiche historische Datenmengen zur Portfoliooptimierung nach Markowitz erforderlich. Aus diesem Grund wurde das Markowitz-Verfahren bisher fast ausschließlich im institutionellen Asset Management eingesetzt. |
|
|